初級シスアド過去問題|平成16年春期午前|問50解説

スポンサードリンク

解答：ア

年代に対して、メモリ容量は10^ｘ乗で増加している。縦軸がメモリの容量の常用対数であるグラフは直線になる。

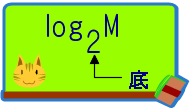
対数とは非常に大きな数値の計算を行うときに用いられる。2ⁿ＝Mという式があるとき、2ⁿ＝Mを満たすMのことを2を底とするMの対数といい以下のように表す。

log₂M

例えば2を底とする16の対数はlog₂16＝4である。これは2を何回掛けたら16になるかということを表している。ちなみに2を底とする256の対数はlog₂256＝8である。

対数の中で10を底とする対数を特に常用対数という。例えばlog₁₀100の常用対数は,10を2回掛ければ100である。したがって2である。常用対数の場合は底の10を省略してlog100と表すこともある。

各年代のメモリ容量の常用対数を求める前に1つだけ以下の対数の公式を覚えて欲しい。

log_aM^t＝t・log_aM
指数は前にくると覚える。

例えばlog₁₀10³は以下のように計算できる。

3×log₁₀10

log₁₀10は1である。(10を何回掛ければ10になるかを考えればよい)

＝3×1

＝3

では、各年代のメモリ容量の常用対数を求めよう。分かりやすくするため各年代をkバイトで表し、その常用対数を求める。

例えば1950年代であれば、以下のようになる。

10k＝10¹k

log₁₀10¹

＝1×log₁₀10¹

＝1×1

＝1

同じようにして各年代のメモリ容量を常用対数を求めたものが以下の表である。

単位　バイト
年代	1950年代	1960年代	1970年代	1980年代	1990年代	2000年代
メモリ容量	10k	100k	1M	10M	100M	1G
ｋバイト	10¹k	10²k	10³k	10⁴k	10⁵k	10⁶k
常用対数	1	2	3	4	5	6

この表からも縦軸をメモリ容量の常用対数、横軸を年代としたときのグラフは直線であることが分かる。

情報技術者試験関連の問題: リクルートが運営するキーマンズネットは最初に無料会員登録が必要ですが、ITパスポート試験や基本情報技術者試験で役に立つIT関連の問題を解くことができます。また、IT関連用語を調べるときにIT単語帳はたいへん便利です。情報処理技術者試験合格、スキルアップのためにぜひ、無料会員登録をしておきたいサイトです。
基本情報技術者講座: 基本情報技術者対策のWebサイトです。
ITパスポート試験情報: ITパスポート試験対策のWebサイトです。

初級シスアド過去問題