初級シスアド過去問題 解答・解説
解答:ウ
スポンサードリンク
この問題のように与えられた制約条件のもとで、結果が最大または最小になるケースを求める手法を線形計画法という。
初級シスアドでは線形計画法に関する問題がここ近年出題されている。線形計画法はどういうときに用いられるかということを押さえておきたい。
いきなり販売利益を求めようとせず稼働時間に注目することがこの問題を解くうえでのポイントである。以下の手順で販売利益を求める。
- 機械P、機械Qと稼働時間の関係を式で表す(制約条件と目的関数)
- 機械Pと機械Qの生産数を求める
- 販売利益を求める
製品Mの生産数をx、製品Nの生産数をyとする。機械P、機械Qと稼働時間は以下の式で表される。分単位で計算を行うので200時間を分にして12,000分としている。
機械P:30x+15y≦12,000(200時間)・・・P
機械Q:20x+30y≦12,000・・・Q
また、生産数であるためx≧0、y≧0である。
利益は以下の式で求められる。
利益=2,500x+3,000y
PとQのように条件を表した式を制約条件という。また、目的を表す式を目的関数という。ここでは利益を求める式が目的関数である。線形計画法は、制約条件のもとで目的関数が最大または最小になる値を求めることである。
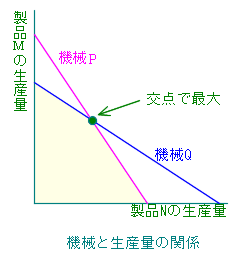
機械と生産数の関係を表したものが右のグラフである。グラフを見ると、二つの式の交点が最大生産数である。したがって、この二つの式を連立一次方程式として解く。解き方としては、xまたはyを消去することを考え、いずれかの式をn 倍する。これを加減法という。
この問題の場合は、Qの15yを30yにしてyを消去する。こためPを2倍する。
60x+30y=24,000
20x+30y=12,000
P−Qを計算する。
40x=12,000
x=300
x=300をPに代入してyを求める。
30×300+15y=12,000
y=200
利益は、製品Mを300個、製品Nを200個生産したときに販売利益が最大になる。したがって、販売利益は以下の式で求められる。
2,500×300+3,000×200=1,350,000円
