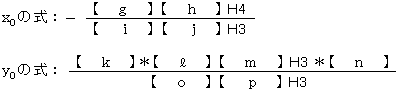| ■問7■ |
|
データ分析に関する次の記述を読んで,設問1〜4に答えよ。
Rさんは日用品販売店に勤務し,販売企画を担当している。企画立案につながる販売データの分析手法を習得する目的で,“データ分析講座”
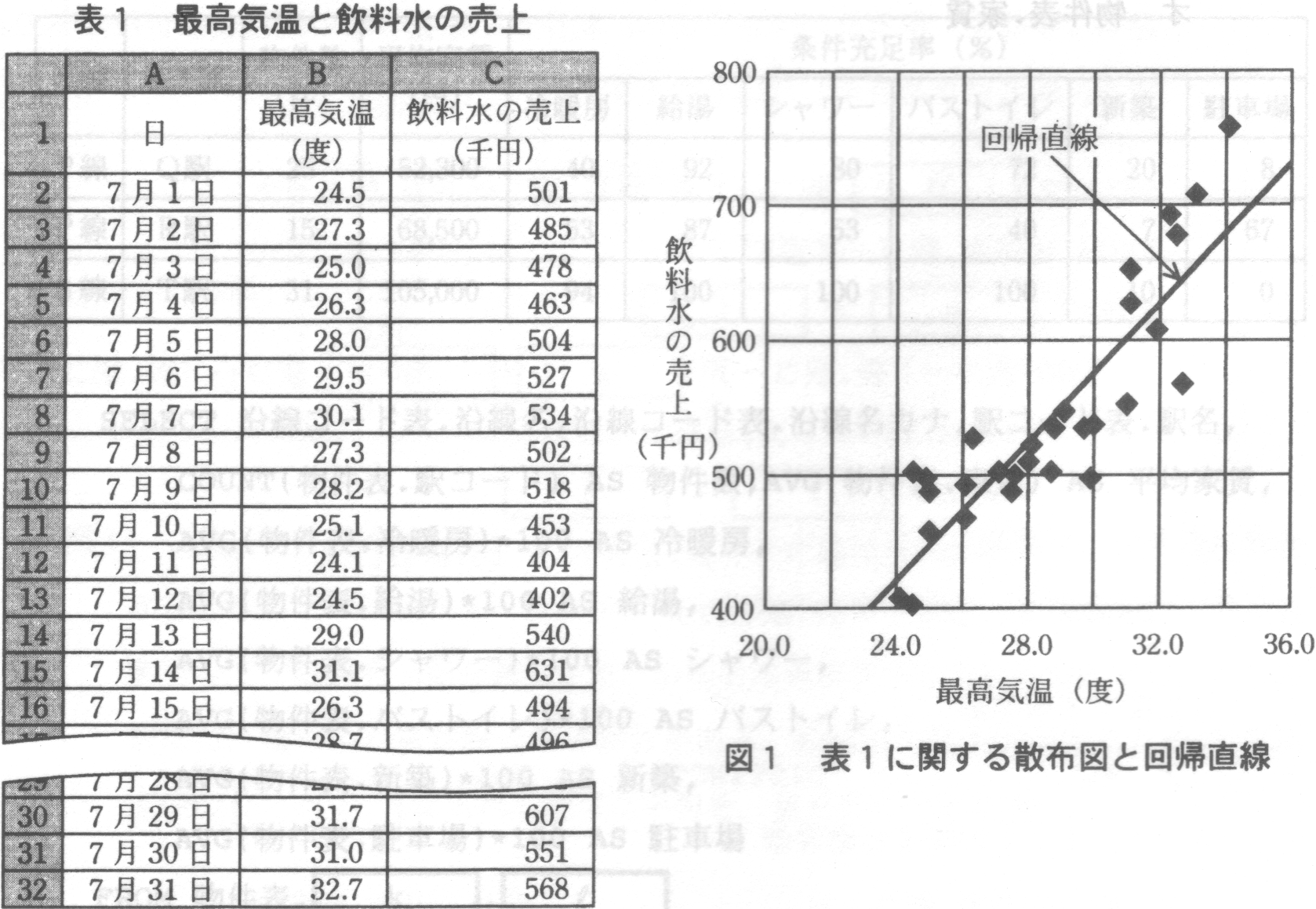
の研修を受講中である。例題として,“ある地区の最高気温とその地区内のコンビニエンスチェーン店での飲料水の売上”(表1)
の関係について表計算ソフトを使って分析している。
散布図を作成すると,最高気温が高いほど飲料水の売上が多い傾向が読み取れる。その傾向を直線で示す
“回帰直線” を描いた(図1)。Rさんは,回帰直線を学んだので,予想最高気温から飲料水の売上を予測することができそうだと考えた。
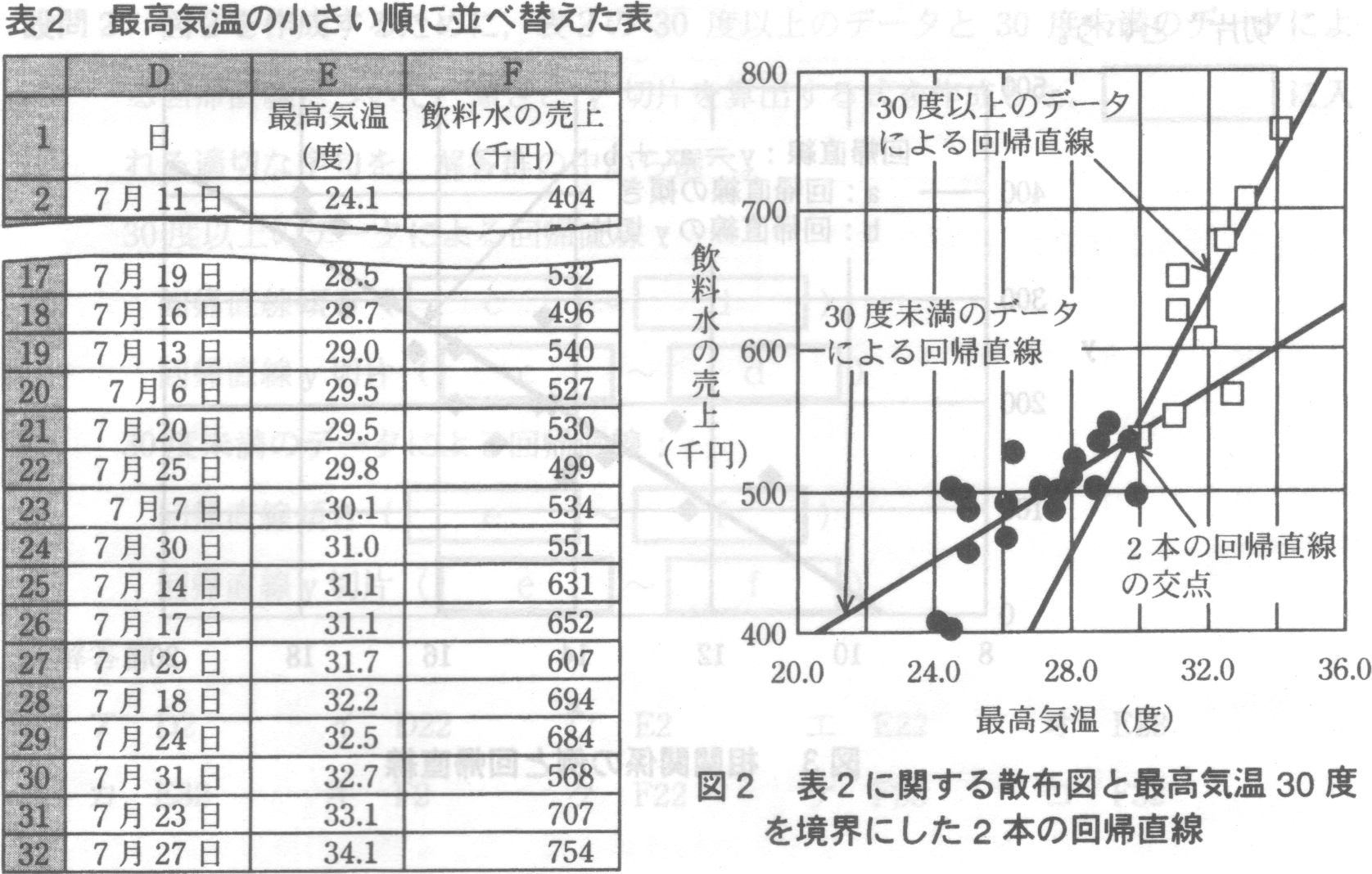
Rさんは散布図を見て,“最高気温が高いほど売上が大きいが,30度あたりを境界にして,その傾向が違っているのではないか”
と考えた。そこで,最高気温30度を境界にして,回帰直線を2本描くことにした。Rさんは,表1の数値を列D〜Fにコピーし,最高気温の小さい順に並べ替え(表2),最高気温30度を境界気温にして,30度以上のデータによる回帰直線と30度未満のデータによる回帰直線の2本を描いた(図2)。
〔回帰直線について〕
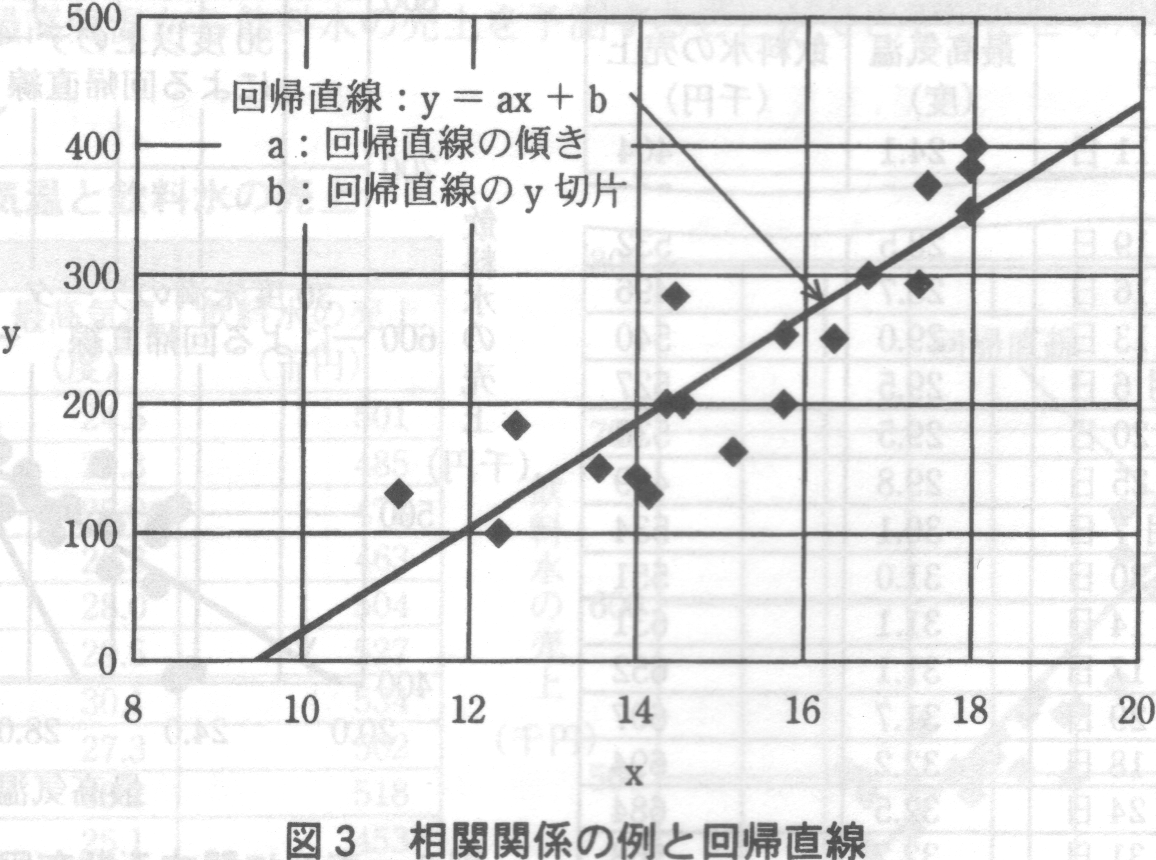
図3の各点のようにxとyの数値の組合せが複数あり,x値が大きいほどy値が大きい傾向のとき,“xとyには正の相関関係がある”
という。xとyに相関関係があるとき,その関係を直線で表現するために,“回帰直線”
( y=ax+b
)を描くことがある。回帰直線とは,各点のy値とそのx値での回帰直線の値との差の二乗を,全部の点について合計したもの(以下,“残差二乗和”
という)
が最小になるように求めた直線である。この求め方を “最小二乗法”
といい,a を回帰直線の“傾き”,b を“y切片”
という。
Rさんが使用している表計算ソフトで使用できる回帰直線に関する関数の説明と使用例を次に示す。ここで,これらの関数は2列の長方形のセル範囲を引数とし,各行の左側の列をx値,右側の列をy値とする。セル範囲は
“左上〜右下” の形で指定する。
| 回帰直線傾き(M1〜N20) |
: |
M列をx値,N列をy値とし,20組の数値について最小二乗法で回帰直線の傾きを算出する。 |
| 回帰直線y切片(M1〜N20) |
: |
同様に最小二乗法で回帰直線のy切片を算出する。 |
| 回帰直線残差二乗和(M1〜N20) |
: |
同様に最小二乗法で求めた回帰直線についての残差二乗和を算出する。 |
|
|
■設問1■
|
図1を作成するために,表1について回帰直線の傾きとy切片を求める次の式を作成した。【 】
に入れる適切な字句を,解答群の中から選べ。
| 傾きを求める式 |
: 回帰直線傾き(【 a 】〜【 b 】) |
| y切片を求める式 |
: 回帰直線y切片(【 a 】〜【 b 】) |
| ア A2 |
イ A32 |
ウ B2 |
エ B32 |
オ C2 |
カ C32 |
|
|
■設問2■
|
図2を作成するために,表2の30度以上のデータと30度未満のデータによる回帰直線について,傾きとy切片を算出する式を作成した。【 】
に入れる適切な字句を,解答群の中から選べ。
| 30度以上のデータによる回帰直線
: |
回帰直線傾き(【 c 】〜【 d 】)
回帰直線y切片(【 c 】〜【 d 】) |
| 30度未満のデータによる回帰直線
: |
回帰直線傾き(【 e 】〜【 f 】)
回帰直線y切片(【 e 】〜【 f 】) |
| ア D2 |
イ D22 |
ウ E2 |
エ E22 |
オ E23 |
| カ E32 |
キ F2 |
ク F22 |
ケ F23 |
コ F32 |
|
|
■設問3■
|
Rさんは境界気温の近辺で売上が連続的に変化するのが自然であろうと考え,2本の回帰直線の交点が,想定した境界気温の近くにあるかどうかを調べることにした。境界気温を30度とし,30度以上のデータによる回帰直線の傾きがセルH1,y切片がセルH2, 30度未満のデータによる回帰直線の傾きがセルH3,y切片がセルH4に計算されているとする。 H1とH3が等しくないとき,2本の回帰直線の交点
( x0 ,y0
) を求める次の式の
【 】 に入れる適切な字句を,解答群の中から選べ。解答は重複して選んでもよい。
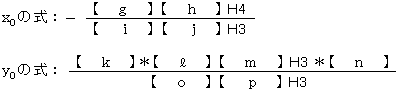
|
|
■設問4■
|
Rさんは30度が適切な境界気温とは限らないと思い,26度,28度,30度,32度の4種類の境界気温について,それぞれ境界気温以上のデータと境界気温未満のデータを使って2本の回帰直線を描いた。4種類の境界気温のうちどれが最も適切か,残差二乗和を使って評価することにした。境界気温以上のデータに対する残差二乗和と境界気温未満のそれとの合計を使って判断するとき,適切なものを解答群の中から選べ。
| ア |
残差二乗和の合計の最も大きい境界気温を選択する。 |
| イ |
残差二乗和の合計の最も小さい境界気温を選択する。 |
|
|
■答え■
|
| 設問1 : |
a−ウ,b−カ, |
| 設問2 : |
c−オ,d−コ,e−ウ,f−ク |
| 設問3 : |
g−イ,h−イ,i−ア,j−イ,k−ア*,ℓ−エ*,m−イ,n−イ,o−ア,p−イ
(*
k,ℓ
は順不同 ) |
| 設問4 : |
イ |
|
|
|
|