| ■問7■ | ||||||||||
|
成績採点表の作成に関する次の記述を読んで、設問1〜5に答えよ。
I教授は、ある大学でドイツ語の授業を担当し、100人の学生に教えている。
成績点の分布を見たI教授は、計算方法はまずまずだと思った。しかし、このような処置は今回限りとし、指導方法や試験問題が適切であったかどうかを調べて、根本的な解決をしたいと考えている。 |
||||||||||
| ■設問1■ | ||||||||||
|
評価試算表において、最多出席者の出席点が 10点になるような計算式をセル D8 に入れ、セル D9
〜 D107 に複写した。計算式の【 】に入れる適切な字句を、解答群の中から選べ。
aに関する解答群
b,dに関する解答群
cに関する解答群
eに関する解答群 |
||||||||||
| ■設問2■ | ||||||||||
|
評価試算表において、筆記点、合計点、補正後合計点、成績点が
60 点以上の人数を調べる計算式をセル E5 に入れ、セル
F5〜H5に複写した。また、59点以下の人数は 100−E5
で求めることにし、計算式を E6 に入れ、セル F6〜H6
に複写した。セル E5
に入れた計算式の【 】に入れる適切な字句を、解答群の中から選べ。 |
||||||||||
| ■設問3■ | ||||||||||
|
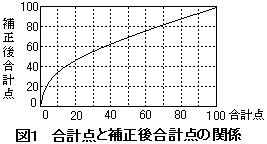
評価試算表において、補正後合計点を求める計算式をセル
G8 に入れ、セル G9〜G107
に複写した。計算式の【 】に入れる適切な字句を、解答群の中から選べ。 整数部(【 j 】) 解答群 ア F8+100−F2 イ F8+60−F3 ウ 平方根(F8)*10 エ 平方根(F8+F4)*10 |
||||||||||
| ■設問4■ | ||||||||||
|
評価試算表において、補正後合計点を最下位の1けたで二捨三入、七捨八入して
5
点刻みにし、成績点を求めるための計算方式を、最下位けたが
0〜2 は 0 に、同 3〜7 は 5 に、同 8〜9 は 10
にする、というように考えた。その計算式をセル H8
に入れ、セル H9〜H107
に複写した。計算式の【 】に入れる適切な字句を、解答群の中から選べ。 |
||||||||||
| ■設問5■ | ||||||||||
|
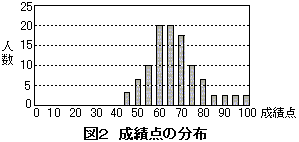
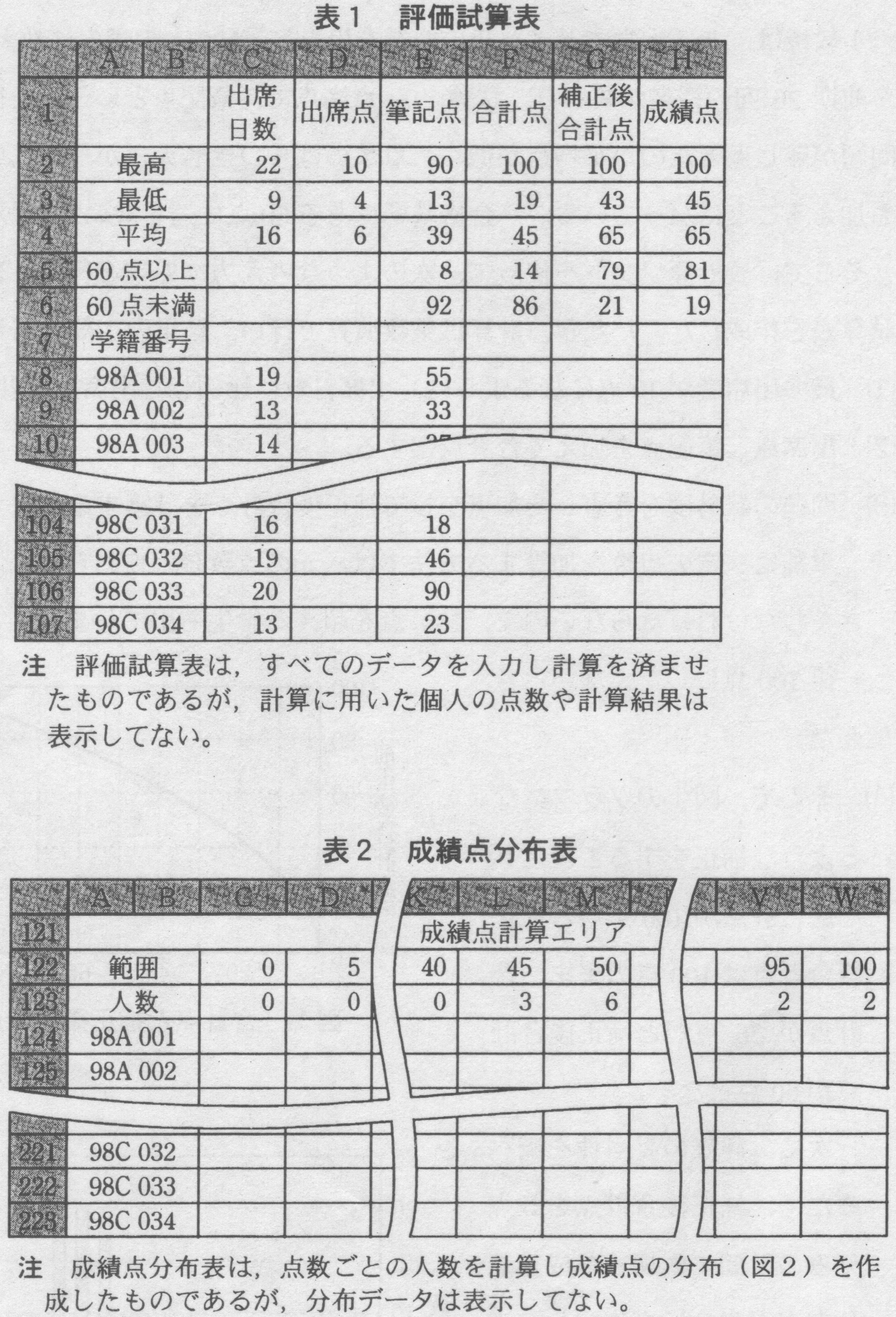
成績点の分布状況を調べるために表2の成績点分布表を作成した。まず、成績点の範囲
0〜100 を 5
ずつで区切り、範囲列の見出しとしてセル
C122〜W122に設定した。次に、一人一人の成績点がどの範囲列に属しているかを調べ、成績点と範囲列の合致するセルは
“1” 、合致しないセルは “空白セル”
とすることにした。計算式をセル C124
に入れ、C124〜W223
に複写した。計算式の【 】に入れる適切な字句を、解答群の中から選べ。 IF(【 r 】【 s 】【 t 】,1,’’) その後、各得点に所属する人数を合計して、図2の成績点の分布を作成した。 r,tに関する解答群 ア H8 イ H$8 ウ $H8 エ $H$8 オ C122 カ C$122 キ $C122 ク $C$122 sに関する解答群 ア = イ < ウ > エ ≠ |
||||||||||
| ■答え■ | ||||||||||
|
||||||||||