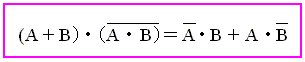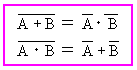| ■問1■ |
|
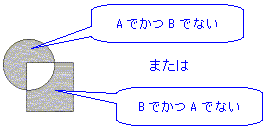
正解:ウ それぞれ塗りつぶされた部分の意味は次のとおりである。
AでかつBでない → A・B
|
| ■問2■ |
|
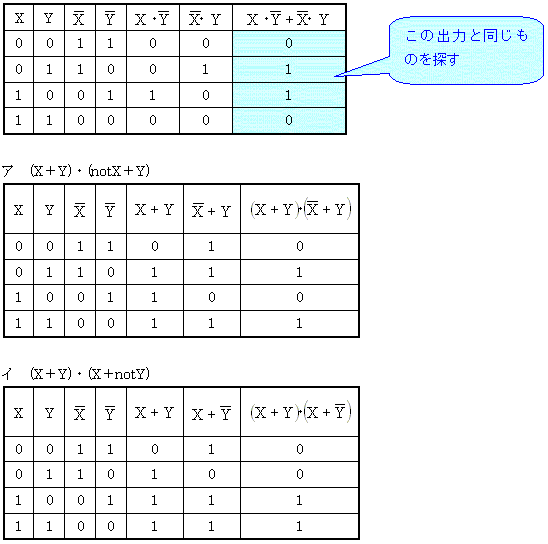
正解:ウ 真理値表を作成し、結果が同じものをさがせばよい。まず、問題のX・notY+notX・Yの真理値表を作成する。なお、ここでは、notXをX 、notYをY と表記している。
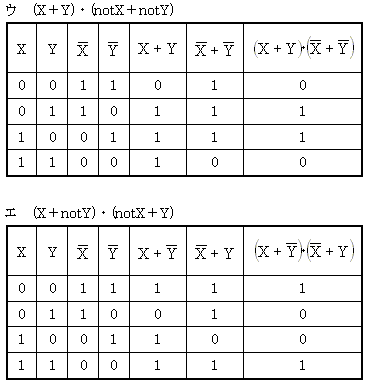
それぞれの真理値表の出力を見れば分かるように(ウ)が問題文の論理式と同じ出力である。この問題では、真理値表を使って解答を求めた。問題の真理値表を見れば分かるように問題の論理式は排他的論理和である。排他的論理和の論理式を覚えておくと簡単に解答を得ることができる。
余談であるが、解答群の(エ)のように入力された値が同じときに「1」を出力するような論理回路をEQV(一致)という。EQVはEORの出力を否定(NOT)したものである。
|
| ■問3■ |
|
正解:ウ 問2(平成9年度 午前 問57)と同じように真理値表を作成して、出力が同じものをさがしてもよい。ド・モルガンの定理を知っていると簡単に解答が得られる。ド・モルガンの定理とはつぎのとおりである。 ド・モルガンの定理にあてはめて解答群を見ると、 X + Yと等しいのは、(ウ)のX ・ Y であることが分かる。
|
| ■問4■ |
|
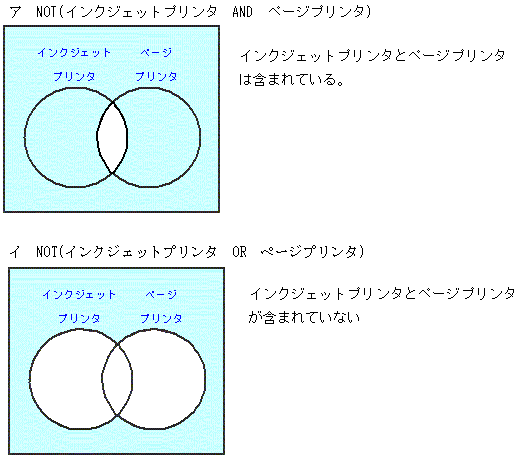
正解:イ 条件を否定(NOT)したときの状態を理解すると間違いにくい。解答群において、勘違いしやすいアとイの、条件を否定している部分のベン図で図示すると、次のとおりである。 ウは、インクジェットプリンタを除くプリンタが検索される。つまり、ページプリンタも含まれてしまう。 エは、
|
| ■問5■ |
|
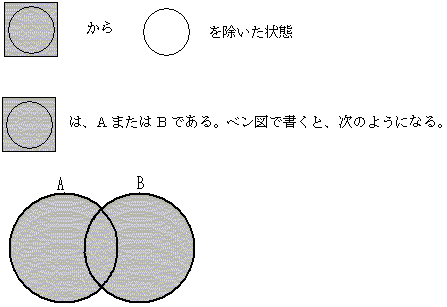
正解:ウ 状態2は、すべて塗りつぶされた状態から、AかつBの部分を除いた状態であると考えることができる。 このベン図は、Aであって、Bでない。または、BであってAでない。つまり、排他的論理和のことである。
|
| ■問6■ |
|
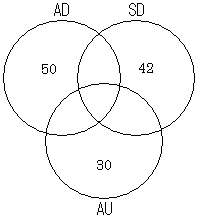
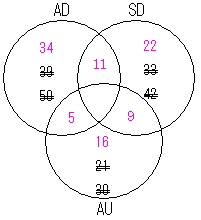
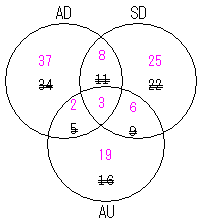
正解:イ 問題文よりベン図を作成すればよい。まず、問題文の「初級システムアドミニストレータ(AD)は50人,上級システムアドミニストレータ(SD)は42人,システム監査技術者(AU)は30人であった。」の人数を記入する。
次に「また,SDの合格者の中に,AUが9人,ADが11人いて,AUの合格者の中にADが5人いた。」の人数を記入する。ここで注意しなくてはいけないのは、重複している人数をそれぞれひいてやらなければならないということだ。
最後に「これらすべての試験に合格している者は3人であった。」の人数を記入する。重複している部分はすべての試験に合格している人間は含まれないので、引かなければならない。また、AD、SDとAUの合格者の人数にそれぞれ加えてやらなければならない。
最終的に求められた人数の合計が1つ以上の試験に合格している社員の人数である。 37人 + 8人 + 25人 + 2人 + 3人 + 6人 + 19人 = 100人
|
| ■問7■ |
|
正解:イ 条件を否定(NOT)したときの状態を理解すると間違いにくい。解答群において、勘違いしやすいアとイの、条件を否定している部分のベン図で図示すると、次のとおりである。 ウは、インクジェットプリンタを除くプリンタが検索される。つまり、ページプリンタも含まれてしまう。 エは、
|
| ■問8■ |
|
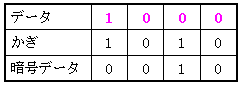
正解:イ かぎと暗号データからそれぞれのけたの排他的論理和論理和を求めればよい。排他的論理和は2つの値が一致しているとき(0と0または、1と1)は0を出力し、2つの値が違うとき(0と1または、1と0)のとき1を出力する。
|
|
Copyright (C) 2002 Pursue Inc., All Rights Reserved |