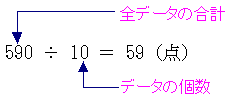初級シスアド講座 統計
|
統計で使用される各種数値の求め方とその意味を次の例題を使って考えていこう。 |
|||||||||||||||
| 1.平均 | |||||||||||||||
|
平均には、単純算術平均と加重算術平均がある。一般に用いられる“平均”は、前者の単純算術平均のことである。ここでは単純算術平均(以下、平均)について解説する。 まず、平均点を求めるためにそれぞれの「得点×人数」を計算し、その合計を求める。
合計すると、590点となる。これを人数の10で割れば、平均点が出る。 平均点は、59点である。 |
|||||||||||||||
| 2.モード(最頻値) | |||||||||||||||
|
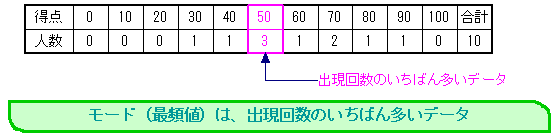
モード(最頻値)は、出現回数のいちばん多いデータのことである。この場合は、いちばん人数が多い点数のことだ。50点が3人でいちばん多い。したがって、モードは50点である。
|
|||||||||||||||
| 3.メジアン(中央値) | |||||||||||||||
|
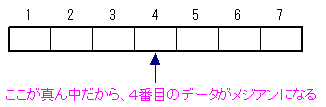
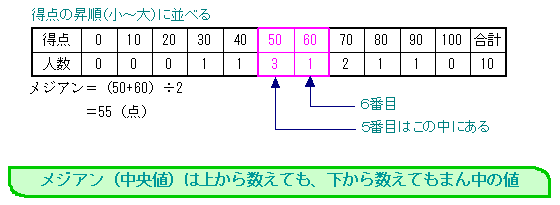
メジアン(中央値)は、データを昇順(小→大)または降順(大→小)に並べたときの中央の値のことである。つまり、上から数えても下から数えてもまん中の値ということだ。 データ数が偶数個のときは、データ数を2で割ったデータとその次のデータの平均をとった値がメジアンである。たとえば、データ数が10ならば、メジアンは、 10 ÷ 2 = 5番目 5番目とその次の6番目の値の平均がメジアンである。 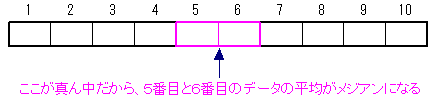
データ数が奇数個のときは、データ数を2で割り小数点以下を切り上げた値がメジアンである。たとえば、データ数が7ならば、 この場合は、すでに得点の昇順に並んでいるので並べ替えをおこなう必要はない。10人のまん中ということだから、5番目と6番目の間になる。したがって、5番目と6番目の平均を取る。5番目は、50点、6番目は60点であるから、平均は(50+60)÷2=55点である。したがって、メジアンは、55点である。 |
|||||||||||||||
| 4.レンジ | |||||||||||||||
レンジ(範囲)は、データ中の最大値から、最小値を引いた値である。この場合は、最大値は90点、最小値は30点である。したがって、レンジは、90 − 30 = 60(点)である。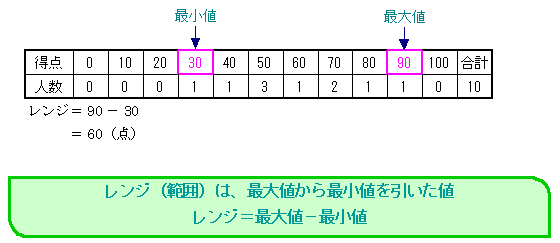
|
|||||||||||||||
| 5.分散 | |||||||||||||||
|
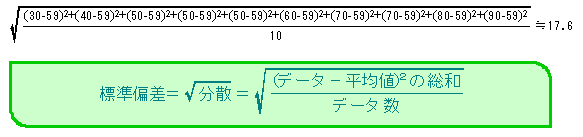
分散は、平均値を中心にしたデータのバラツキの大小を見るときに使われる。この数値が大きいとバラツキが大きいと判断できる。バラツキが大きいということは、平均値を中心にデータが広い範囲にちらばっているということである。逆にこの数値が小さいとバラツキが小さいと判断できる。バラツキが小さいとは、平均付近にデータがかたまっているということである。 分散は、それぞれのデータにおいて“(データ−平均値)2”を計算し、その総和をデータ数で割った値である。なお、“データ−平均値”のことを偏差という。 偏差=データ−平均値 |
|||||||||||||||

このように書かれている場合は、データを1つずつ書くと考えやすい。データを1つずつに書き直すとつぎのようになる。 分散を求める |
|||||||||||||||
| 6.標準偏差 | |||||||||||||||
|
平均値を中心にしたデータのバラツキの大小を見るときに使われる指標として分散がある。そのほかに標準偏差がある。標準偏差は、分散の平方根である。標準偏差のほうが分散に比べてて平方根を求めるぶん計算は複雑になるが、データと同じ尺度で分かりやすい。
|
|||||||||||||||
| 7.正規分布 | |||||||||||||||
|
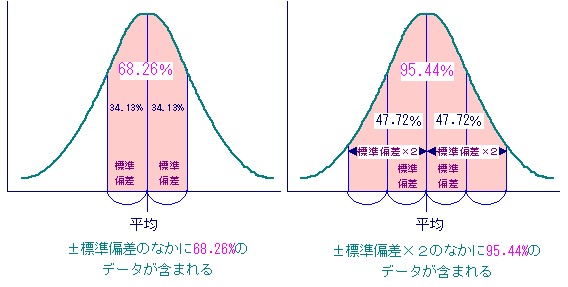
正規分布とは、つぎの図のように平均を中心に左右対称の“つりがね型”をした分布のことである。つぎの図は平均が50、標準偏差が10の正規分布である。
|
|||||||||||||||
|
データが正規分布になっていると、±標準偏差の範囲に68.26%のデータ含まれ、±標準偏差×2の範囲に95.44%のデータが含まれる。 テスト結果を分析するときに使われる“偏差値”はこの正規分布からきている。偏差値とは、全体のなかでどの位置にいるのかを把握するときに使われる尺度だと考えて欲しい。なお、偏差値は、データが正規分布になっていないと意味がない。 これで平均点に対して、どの位置にいるのかが分かる。 |
|||||||||||||||
|
|||||||||||||||
|
|
|||||||||||||||